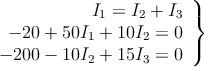Sistema resuelto por Gauss. Ejercicio 4439

|

Resuelve por el método de Gauss el siguiente sistema de ecuaciones

\left. \begin{array}{r} I_1=I_2+I_3 \\ -20+50I_1+10I_2=0 \\ -200-10I_2+15I_3=0 \end{array} \right \}

SOLUCIÓN

Primero ordenamos el sistema y lo expresamos en forma matricial

\left. \begin{array}{r} I_1-I_2-I_3 =0 \\ 50I_1+10I_2=20 \\ -10I_2+15I_3=200 \end{array} \right \} \quad \left( \begin{array}{ccc|c} 1 & -1 & -1 & 0 \\ 50 & 10 & 0 & 20 \\ 0 & -10 & 15 & 200 \end{array} \right )

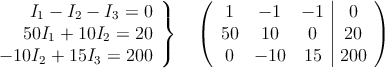
Podemos dividir la Fila 2 entre 10 y la fila 3 entre 5 (quedará más simplificado)

\left( \begin{array}{ccc|c} 1 & -1 & -1 & 0 \\ 5 & 1 & 0 & 2 \\ 0 & -2 & 3 & 40 \end{array} \right ) \begin{array}{c} \: \\ 5 \cdot F_1 - F_2 \rightarrow F_2 \\ \: \end{array} \: \left( \begin{array}{ccc|c} 1 & -1 & -1 & 0 \\ 0 & -6 & -5 & -2 \\ 0 & -2 & 3 & 40 \end{array} \right )

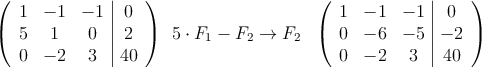
Los cambios siguientes no son obligatorios, pero me van a hacer más fáciles las operaciones:
1) Multiplicar por (-1) la F2 (son todos negativos, se convierten a positivos)
2) Intercambiar F2 y F3 con objeto de que las fracciones sean "medios" en lugar de "sextos"

\left( \begin{array}{ccc|c} 1 & -1 & -1 & 0 \\ 0 & -2 & 3 & 40 \\ 0 & 6 & 5 & 2 \end{array} \right )\:\: \begin{array}{c} \: \\ \frac{F_2}{-2} \rightarrow F_2 \\ \: \end{array} \quad \left( \begin{array}{ccc|c} 1 & -1 & -1 & 0 \\ 0 & 1 & -3/2 & -20 \\ 0 & 6 & 5 & 2 \end{array} \right )

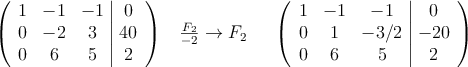
Nos queda el último cambio 6 F_2 - F_3 \rightarrow F_3

\left( \begin{array}{ccc|c} 1 & -1 & -1 & 0 \\ 0 & 1 & -3/2 & -20 \\ 0 & 0 & -14 & -122 \end{array} \right )

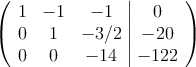
Ahora pasamos a ecuaciones y resolvemos el sistema escalonado "de abajo hacia arriba"

\left\{ \begin{array}{l} I_1 -I_2 -I_3=0 \\ I_2 -\frac{3}{2}I_3 = -20 \\ -14I_3 = -122 \longrightarrow I_3=\frac{-122}{-14} \longrightarrow \textcolor{blue}{I_3=\frac{61}{7}} \end{array} \right.

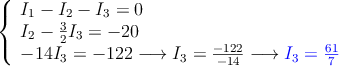
Ahora en la segunda ecuación:

I_2 -\frac{3}{2}I_3 = -20
I_2 -\frac{3}{2} \cdot \frac{61}{7} = -20
I_2 = -20 + \frac{183}{14} \longrightarrow \textcolor{blue}{I_2=\frac{-97}{14}}

Finalmente en la primera ecuación:

I_1 -I_2 -I_3=0
I_1 - \frac{-97}{14} -\frac{61}{7}=0
I_1 = \frac{-97}{14} +\frac{61}{7}=0 \longrightarrow \textcolor{blue}{I_1=\frac{25}{14}}