Estadística Distribución Binomial

|

Un tirador hace blanco en 3 de cada cuatro disparos. Si realiza 9 disparos:

– a) Probabilidad de acertar al menos 8
– b) ¿Cuál es el número esperado de aciertos?

SOLUCIÓN

Se trata de un Binomial donde el experimento se repite 9 veces (n=9) y la probabilidad de éxito es 3/4 \left(p=\frac{3}{4}=0.75\right)

X \longrightarrow B(9,0.75)

Nos están pidiendo que acierte 8 o más veces, es decir P(X \geq 8)

P(X \geq 8) = P(X=8) + P(X=9)

LA fórmula que usamos en la binomial es la siguiente:

P(X=k) = \left( \begin{array}{c} n \\ k \end{array} \right) \cdot p^k \cdot(1-p)^{n-k}

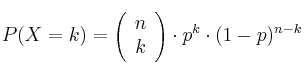
La aplicamos a nuestro caso particular

P(X=8) = \left( \begin{array}{c} 9 \\ 8 \end{array} \right) \cdot 0.75^8 \cdot 0.25^1=9 \cdot 0,1001 \cdot 0.25 = 0.225

P(X=9) = \left( \begin{array}{c} 9 \\ 9 \end{array} \right) \cdot 0.75^9 \cdot 0.25^0=1 \cdot 0,075 \cdot 1 = 0.075

P(X \geq 8) = P(X=8) + P(X=9) = 0.225+0.075 = \fbox{0.3}

b) ¿Cuál es el número esperado de aciertos?

El número esperado (media o esperanza matemática) de la Binomial es n \cdot p, que en nuestro caso será 9 \cdot 0.75=\textcolor{blue}{6.75}

Podemos decir que el número esperado de aciertos es 7