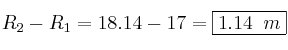Geometría Área corona circular

|

Queremos construir una acera alrededor de un parque circular. El diámetro del parque es de 34 m. Si el área de la acera es 40 \pi m^2, calcule su ancho.

SOLUCIÓN

Recordemos previamente que el radio es la mitad del diámetro y que el áea de un círculo es A = \pi\cdot Radio^2
Hacemos un dibujo con los datos del problema

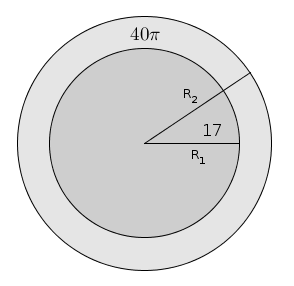
Área_acera = Area_círculo_grande - Área_parque
40 \pi = \pi \cdot {R_2}^2 - \pi \cdot 17^2
40 \pi = \pi \cdot ({R_2}^2 - 17^2)
Podemos simplificar dividiendo por \pi ambos miembros de la igualdad
40= {R_2}^2 - 17^2
40+17^2= {R_2}^2
329= {R_2}^2
R_2 = \sqrt{329} \simeq 18.14 \: m

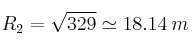
La anchura de la acera es el radio grande menos el radio pequeño
R_2-R_1 = 18.14 - 17 = \fbox{1.14 \: m}