Probabilidad al lanzar dos dados

|

Lanzamos dos dados. Calcula la probabilidad de que:

a) salgan dos números iguales
b) salgan dos múltiplos de 3
c) la suma de los puntos de los dos números obtenidos sea mayor o igual a 10
d) la suma de los puntos de los dos números obtenidos sea mayor o igual a 9
e) la suma de los puntos de los dos números obtenidos sea menor o igual a 5
f) la suma de los puntos de los dos números obtenidos sea menor o igual a 4

SOLUCIÓN

Espacio muestral al lanzar dos dados
Al lanzar dos datos hay 36 casos distintos
matematicasies.com

Al lanzar dos dados, el espacio muestral estaría compuesto de 6 \cdot 6 = 36 sucesos elementales:

E = \{ (1-1) (1-2) (1-3) (1-4) \cdots (2-1) (2-2) \cdots (6-5) (6-6) \}

a) salgan dos números iguales
Hay 6 casos: (1-1) (2-2) (3-3) (4-4) (5-5) (6-6) de los 36 posibles, por tanto la probabilidad es \textcolor{blue}{\frac{6}{36}}

b) salgan dos múltiplos de 3
Hay 4 casos: (3-3) (3-6) (6-3) (6-6) de los 36 posibles, por tanto la probabilidad es \textcolor{blue}{\frac{4}{36}}

c) la suma de los puntos de los dos números obtenidos sea mayor o igual a 10
En la siguiente tabla representamos todas las sumas posibles

\begin{tabular}{c|c|c} Suma & Probabilidad & Casos\\ \hline 2 & 1/36 & (1-1)\\ \hline 3 & 2/36 & (1-2) (2-1)\\ \hline 4 & 3/36 & (1-3) (2-2) (3-1) \\ \hline 5 & 4/36 & (1-4) (2-3) (3-2) (4-1)\\ \hline 6 & 5/36 & (1-5) (2-4) (3-3) (4-2) (5-1)\\ \hline 7 & 6/36 & (1-6) (2-5) (3-4) (4-3) (5-2) (6-1)\\ \hline 8 & 5/36 & (2-6) (3-5) (4-4) (5-3) (6-2)\\ \hline 9 & 4/36 & (3-6) (4-5) (5-4) (6-3) \\ \hline 10 & 3/36 & (4-6) (5-5) (6-4)\\ \hline 11 & 2/36 & (5-6) (6-5)\\ \hline 12 & 1/36 & (6-6)\\ \hline \end{tabular}

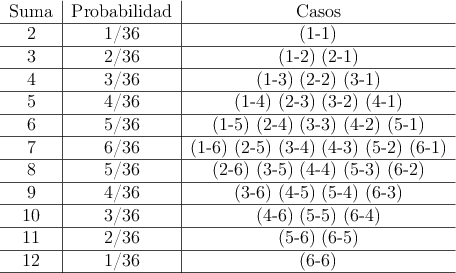
Sea S = "suma de los puntos de los dos dados". Entonces:

c) P(S \geq 10) = \textcolor{blue}{\frac{6}{36}}

d) P(S \geq 9) = \textcolor{blue}{\frac{10}{36}}

e) P(S \leq 5) = \textcolor{blue}{\frac{10}{36}}

e) P(S \leq 4) = \textcolor{blue}{\frac{6}{36}}