Problemas que se resuelven con ecuaciones

Encuentra un número cuyo cuadrado sea igual al cuadrado del número anterior más 23 unidades.

SOLUCIÓN

Asignamos incógnitas a los datos que nos pidan

Número desconocido $\longrightarrow x$

Además, debemos recordar que:
Número anterior $\longrightarrow x-1$

Expresamos el enunciado en lenguaje matemático:

$x^2 = x^2 + 1^2 -2 \cdot x \cdot 1+23$

Parece una ecuación de segundo grado.
Pasamos todo al primer miembro

$\cancel{x^2} \cancel{- x^2} +2x -24 = 0$

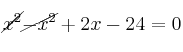
Se queda en una ecuación de primer grado

$x =\frac{24}{2}$

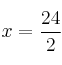
Podemos comprobarlo:

Por tanto es correcto.
El número pedido es el 12