ecuaciones grado superior
Resuelve la ecuación: ![]()
SOLUCIÓN
En primer lugar usamos la regla de Ruffini para ver si hay soluciones enteras:
![\polyhornerscheme[x=1, resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{4x^3-12x^2+11x-3} \polyhornerscheme[x=1, resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{4x^3-12x^2+11x-3}](local/cache-TeX/ed4c98d41edf252cd30b0be8baec1a45.png)
Para el cociente, resolvemos la ecuación de segundo grado
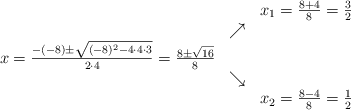
Por tanto, las soluciones de la ecuación son:
![]()
Resuelve la ecuación: ![]()
En primer lugar usamos la regla de Ruffini para ver si hay soluciones enteras:
![\polyhornerscheme[x=1, resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{4x^3-12x^2+11x-3} \polyhornerscheme[x=1, resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{4x^3-12x^2+11x-3}](local/cache-TeX/ed4c98d41edf252cd30b0be8baec1a45.png)
Para el cociente, resolvemos la ecuación de segundo grado
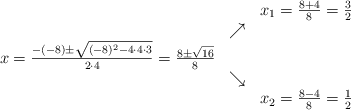
Por tanto, las soluciones de la ecuación son:
![]()