sistemas lineal 2x2

Resuelve el sistema de ecuaciones:

$\displaystyle { \left\{ {x-3y=-1 \atop 3x+6y=2 } \right.}$

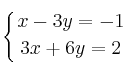
SOLUCIÓN

Resolvemos por el método de reducción

$\begin{array}{cccc} x & -3y & = & -1 \\ 3x & +6y & = & 2 \\ \hline&&& \end{array}$

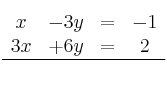
Podemos multiplicar la 1ª ecuación por 2 y así cancelar la incógnita "y"

$\begin{array}{cccc} 2x & -6y & = & -2 \\ 3x & +6y & = & 2 \\ \hline&&& \end{array}$

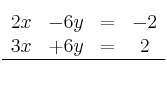
Cancelamos y sumamos ambas ecuaciones:

$\begin{array}{cccc} 2x & \cancel{-6y} & = & -2 \\ 3x & \cancel{+6y} & = & 2 \\ \hline 5x && = & 0 \end{array}$

$5x=0 \longrightarrow x=\frac{0}{5} \longrightarrow \fbox{x=0}$

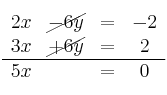
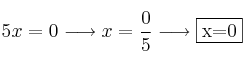
Para calcular "y" podemos usar cualquiera de las ecuaciones, por ejemplo la 1ª ecuación:

$-3y=-1 \longrightarrow y=\frac{-1}{-3} \longrightarrow \fbox{y=1/3}$

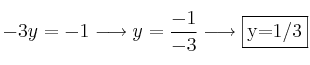
Soluciones: x=0 ; y=1/3