sistemas nolineal 2x2
Resuelve el sistema de ecuaciones:
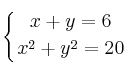
SOLUCIÓN
Se trata de un sistema no lineal (en los sistemas lineales las incógnitas no pueden ir multiplicadas entre sí, ni divididas entre sí, ni elevadas al cuadrado, etc.).
Los sistemas no lineales se suelen resolver por sustitución: despejamos una incógnita en una de las ecuaciones y sustituimos en las demás ecuaciones.
Vamos a despejar "x" en la 1ª ecuación:
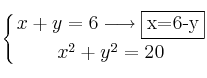
Ahora sustituimos en la 2ª ecuación
![]()
![]()
Aplicamos las fórmulas de los productos notables
![]()
Obtenemos una ecuación de 2º grado que ordenamos
![]()
Se puede simplificar dividiendo todo por 2 (pero no es obligatorio)
Resolvemos aplicando la fórmula
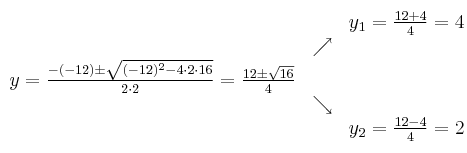
Ahora calculamos "x", que teníamos despejada antes (para cada solución de "y" hay que calcular su correspondiente "x")
– Si ![]()
![]()
Solución: 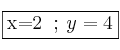
– Si ![]()
![]()
Solución: 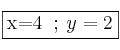
Como vemos, el sistema tiene dos soluciones