04 - Posición relativa de tres planos

|

Dados tres planos en ecuación general:

\pi_1 \equiv A_1x+B_1y+C_1z = D_1
\pi_2 \equiv A_2x+B_2y+C_2z = D_2
\pi_3 \equiv A_3x+B_3y+C_3z = D_3

podemos estudiar su posición relativa discutiendo el sistema de 3 ecuaciones con 3 incógnitas.

Para ello, usaremos el teorema de Ruché, analizando el rango de la matriz de los coeficientes (A) y el rango de la matriz ampliada (A^*).

A|A^*= \left( \begin{array}{ccc} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \end{array} \right. \left| {\begin{array}{c} D_1 \\ D_2 \\ D_3 \end{array} } \right)

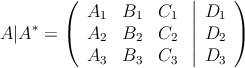
Los casos posibles son:

– r(A)=1 , r(A^*)=1 S.C.I. Los tres planos son coincidentes. Al valer ambos rangos 1, se trata de una misma ecuación del plano
– r(A)=1 , r(A^*)=2 S. Incomp. Los tres planos son paralelos (al ser r(A)=1) y sin ningún punto en común (al ser S.I.). Pueden ser los 3 distintos o bien dos de ellos coincidentes.
– r(A)=2 , r(A^*)=2 S.C.I. Los tres planos se cortan en una recta. Pueden ser dos de ellos coincidentes o los tres distintos
– r(A)=2 , r(A^*)=3 S. Incomp. No tienen ningún punto en común. Se cortan en una recta dos a dos, o bien hay dos paralelos y el tercero corta a ambos.
– r(A)=3 , r(A^*)=3 S.C.D. Tienen un sólo punto en común. Los tres planos se cortan en un punto

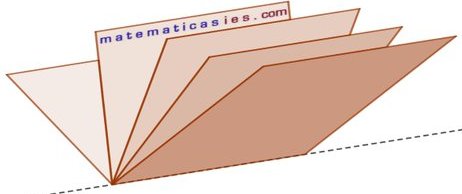
Varios planos cortándose en una recta

Varios planos se cortan en una recta
Posición relativa de 3 planos. Planos con una recta en común
matematicasies.com