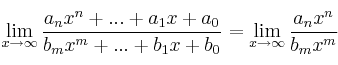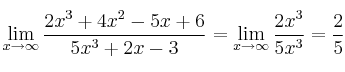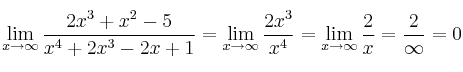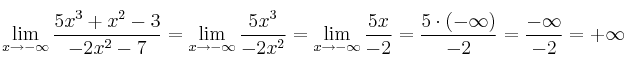Cálculo de límites de funciones racionales cuando x tiende a un infinito
Indeterminación 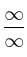
Si 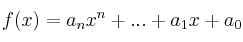
y 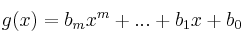 son funciones polinómicas de cualquier grado, entonces:
son funciones polinómicas de cualquier grado, entonces:
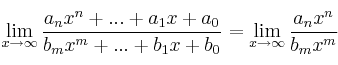
Es decir, basta con tomar los términos de mayor grado (en numerador y denominador) y despreciar el resto.
No obstante, siempre se obtiene una INDETERMINACIÓN del tipo 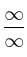
Se resuelve dividiendo numerador y denominador por x elevado al menor de los grados (de numerador y denominador).
Por ejemplo, si grado(numerador)=4 y grado(denominador)=3 dividimos por 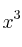
Veamos unos ejemplos:
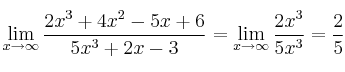
Cuando numerador y denominador son polinomios del mismo grado, el límite es el cociente entre los coeficientes de los términos de mayor grado
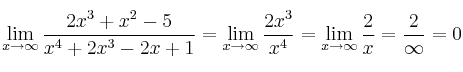
Cuando el grado del denominador es mayor, el límite es siempre cero
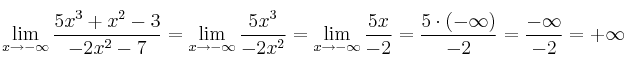
Cuando el grado del numerador sea mayor, el resultado siempre será un infinito
(
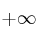
o
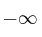
según los coeficientes).
 Introducción al cálculo de límites (gráficamente)
Introducción al cálculo de límites (gráficamente) Cálculo de límites de funciones polinómicas (I)
Cálculo de límites de funciones polinómicas (I) Cálculo de límites de funciones polinómicas (II)
Cálculo de límites de funciones polinómicas (II) Cálculo de límites de funciones racionales (I)
Cálculo de límites de funciones racionales (I) Cálculo de límites de funciones racionales (II)
Cálculo de límites de funciones racionales (II) Cálculo de límites de funciones racionales (III)
Cálculo de límites de funciones racionales (III) Cálculo de límites de funciones racionales (IV)
Cálculo de límites de funciones racionales (IV) Cálculo de límites de funciones irracionales (I)
Cálculo de límites de funciones irracionales (I) Cálculo de límites de funciones irracionales (II)
Cálculo de límites de funciones irracionales (II) Cálculo de límites de funciones irracionales (III)
Cálculo de límites de funciones irracionales (III) Infinitos de diferentes órdenes
Infinitos de diferentes órdenes Indeterminación 1 elevado a infinito
Indeterminación 1 elevado a infinito Indeterminaciones
Indeterminaciones