Una empresa de productos farmacéuticos afirma en su publicidad que uno de sus medicamentos reduce considerablemente los síntomas de la alergia primaveral en
el  de la población. Una asociación de consumidores ha experimentado dicho fármaco en una muestra de 200 socios de la misma, y obtenido el resultado indicado en la publicidad en 170 personas. Determina si la asociación de consumidores puede considerar que la
de la población. Una asociación de consumidores ha experimentado dicho fármaco en una muestra de 200 socios de la misma, y obtenido el resultado indicado en la publicidad en 170 personas. Determina si la asociación de consumidores puede considerar que la
afirmación de la empresa es estadísticamente correcta a un nivel de significación de 0,05
SOLUCIÓN
Contraste bilateral para la proporción (Ver Teoría)
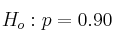 (hipótesis nula: la proporción es
(hipótesis nula: la proporción es 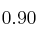 )
)
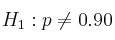 (hipótesis alternativa: la proporción no es de
(hipótesis alternativa: la proporción no es de 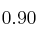 )
)
Datos del problema
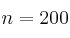
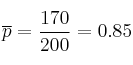
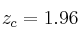 (confianza del
(confianza del 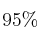 )
)
Región de aceptación (R)
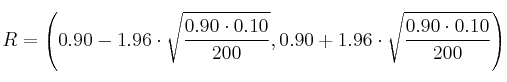
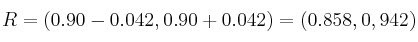
Toma de decisión
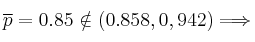 Rechazamos
Rechazamos 
Rechazamos la afirmación de la empresa a un nivel de significación de 0,05
![]() (hipótesis nula: la proporción es
(hipótesis nula: la proporción es ![]() )
)
![]() (hipótesis alternativa: la proporción no es de
(hipótesis alternativa: la proporción no es de ![]() )
)![]()
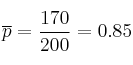
![]() (confianza del
(confianza del ![]() )
)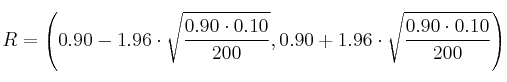
![]()
![]() Rechazamos
Rechazamos ![]()
