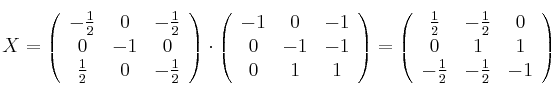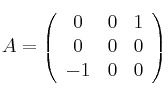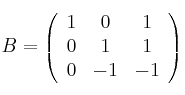Selectividad Andalucía 2002-4-B3

|

Determina la matriz X que verifica la ecuación AX = X-B siendo

A = \left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{array} \right) \qquad y \qquad
B = \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & -1 & -1 \end{array} \right)

SOLUCIÓN

Resolveremos la ecuación matricial usando este método, para el que es necesario saber calcular la inversa de una matriz.

AX = X-B
AX -X= -B
(A-I) \cdot X = -B
(A-I)^{-1} \cdot (A-I) \cdot X =(A-I)^{-1} \cdot (-B)
X =(A-I)^{-1} \cdot (-B)

A-I = \left( \begin{array}{ccc} -1 & 0 & 1 \\ 0 & -1 & 0 \\ -1 & 0 & -1 \end{array} \right)
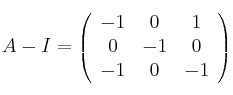
Calculamos la inversa usando la fórmula y obtenemos:

(A-I)^{-1} = \left( \begin{array}{ccc} -\frac{1}{2} & 0 & -\frac{1}{2} \\ 0 & -1 & 0 \\ \frac{1}{2}& 0 & -\frac{1}{2} \end{array} \right)
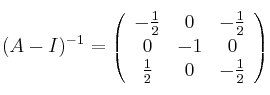
Ya sólo queda multiplicarla por la matriz (-B)
X =(A-I)^{-1} \cdot (-B)
X =\left( \begin{array}{ccc} -\frac{1}{2} & 0 & -\frac{1}{2} \\ 0 & -1 & 0 \\ \frac{1}{2}& 0 & -\frac{1}{2} \end{array} \right) \cdot \left( \begin{array}{ccc} -1 & 0 & -1 \\ 0 & -1 & -1 \\ 0 & 1 & 1 \end{array} \right) = \left( \begin{array}{ccc} \frac{1}{2} & -\frac{1}{2} & 0 \\ 0 & 1 & 1 \\ -\frac{1}{2}& -\frac{1}{2} & -1 \end{array} \right)