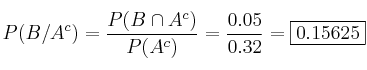Selectividad Andalucía 2013-1-A3
SOLUCIÓN
Datos del problema:
![]()
![]()
![]()
Para resolver el ejercicio debemos conocer el Resumen de Fórmulas de Probabilidad
– a) Nos piden ![]() . Usaremos la foŕmula de la unión:
. Usaremos la foŕmula de la unión:
![]()
donde despejamos ![]() , quedando:
, quedando:
![]()
Conocemos ![]() y
y ![]() . Nos falta por obtener
. Nos falta por obtener ![]() , que lo sacaremos del tercer dato que nos aporta el ejercicio:
, que lo sacaremos del tercer dato que nos aporta el ejercicio:
![]() Aplicando las leyes de Morgan tenemos que
Aplicando las leyes de Morgan tenemos que
![]() Por tanto
Por tanto ![]() . Con todos los datos, basta con aplicarlos a la fórmula:
. Con todos los datos, basta con aplicarlos a la fórmula:
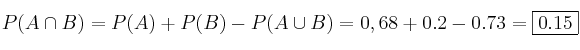
– b) 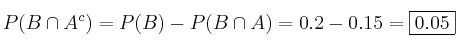
– c)