Ecuaciones del plano 4568

Dados el punto y los vectores $\vec{v}=(2,4,-1)$ y $\vec{w}=(0,-2,3)$ se pide:

a) Halla la ecuación vectorial, paramétrica e implícita (o general) del plano $\pi$ que forman.

b) Comprueba si los puntos y pertenecen o no al plano $\pi$ .

SOLUCIÓN

Ecuación vectorial

$(x,y,z) = (3,-2-1) + \alpha (2,4,-1) + \beta (0,-2,3)$

Ecuaciones paramétricas

$\left\{ \begin{array}{lll} x=3+2\alpha \\ y=-2+4\alpha -2 \beta \\z=1-\alpha + 3\beta \end{array} \right.$

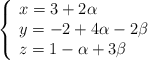
Ecuación implícita o general

$\left| \begin{array}{ccc} x-3 & y+2 & z-1 \\2 & 4 & -1 \\0 & -2 & 3 \end{array} \right| = 0$

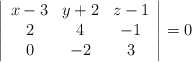
Resolvemos determinante y ordenamos:

$\pi \equiv \color{blue}{ 10x-6y-4z-38=0}$

b) Para comprobar si un punto pertenece a un plano tan sólo haya que mirar si verifica la ecuación del plano

$10 \cdot 3-6 \cdot 2 -4 \cdot 1-38\stackrel{?}{=}0$
$-24 \neq 0$
$A \not \in \pi$

$10 \cdot 1-6 \cdot 3 -4 \cdot (-9)-38\stackrel{?}{=}0$
$-10 \neq 0$
$B \not \in \pi$