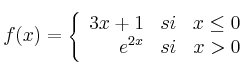-
Aplica el teorema de Bolzano para averiguar si la ecuación 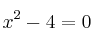 tiene alguna solución en el intervalo
tiene alguna solución en el intervalo ![[1,3] [1,3]](local/cache-TeX/689e1b934020b6eb3917c155d94a9a0f.png)
-
Aplica el teorema de Bolzano para demostrar que la ecuación 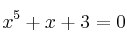 tiene alguna solución.
tiene alguna solución.
-
Aplica el teorema de Bolzano para demostrar que la ecuación 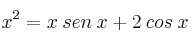 tiene alguna solución en el intervalo
tiene alguna solución en el intervalo ![[0, \pi] [0, \pi]](local/cache-TeX/f74f8710fd31ce502365bc814a7fd3b6.png)
-
Aplica el teorema de Bolzano para demostrar que la ecuación 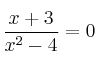 tiene alguna solución en el intervalo
tiene alguna solución en el intervalo ![[1, 3] [1, 3]](local/cache-TeX/ad1ef70ad05826c2944514e28ffb62fa.png)
-
Estudia la continuidad de la siguiente función: