Ejercicios de Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
(110) ejercicios de Matrices, Determinantes y Sistemas
-
Demuestra que
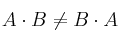 , siendo las matrices
, siendo las matrices
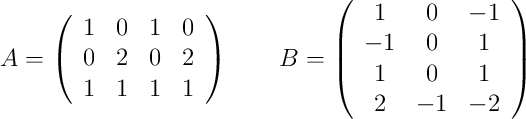
-
Demuestra que
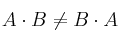 , siendo las matrices
, siendo las matrices
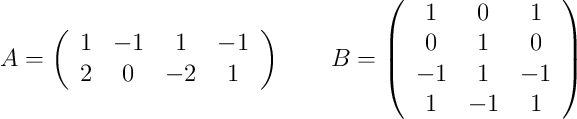
-
Indica si las siguientes matrices son regulares o singulares:
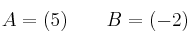
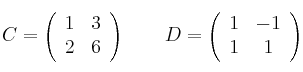
-
Calcula aplicando la Regla de Sarrus el determinante de la siguiente matriz:
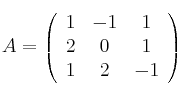
-
Sea la matriz
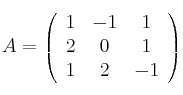
– Calcula su determinante
 Matemáticas IES
Matemáticas IES
