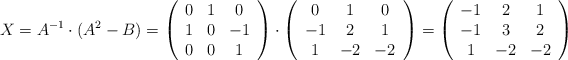Matrices Selectividad Cantabria
Resuelva la ecuación matricial ![]() , siendo las matrices
, siendo las matrices
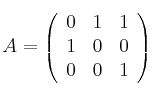 ;
;
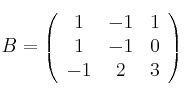
SOLUCIÓN
![]()
![]()
![]()
![]()
![]()
Tenemos que calcular la inversa de A siguiendo este procedimiento y obtendremos:

Además debemos calcular

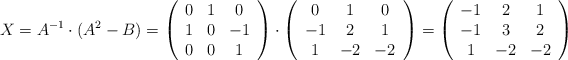
Resuelva la ecuación matricial ![]() , siendo las matrices
, siendo las matrices
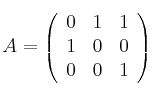 ;
;
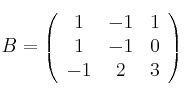
![]()
![]()
![]()
![]()
![]()
Tenemos que calcular la inversa de A siguiendo este procedimiento y obtendremos:

Además debemos calcular