Selectividad Andalucía 2001-3-A1
Calcula 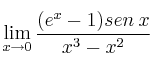
SOLUCIÓN
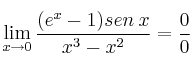
Aplicamos la Regla de L’Hôpital
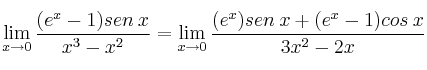
Vuelve a dar ![]() . Volvemos a aplicar L’Hôpital y queda:
. Volvemos a aplicar L’Hôpital y queda:
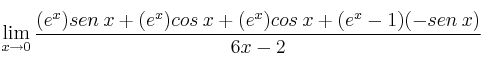
Volvemos a sustituir ![]() por 0 y esta vez ya obtenemos un resultado:
por 0 y esta vez ya obtenemos un resultado: 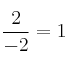
Por tanto: 
Calcula 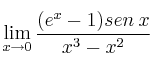
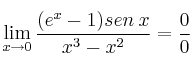
Aplicamos la Regla de L’Hôpital
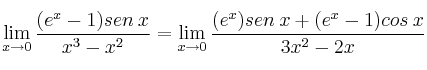
Vuelve a dar ![]() . Volvemos a aplicar L’Hôpital y queda:
. Volvemos a aplicar L’Hôpital y queda:
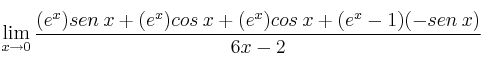
Volvemos a sustituir ![]() por 0 y esta vez ya obtenemos un resultado:
por 0 y esta vez ya obtenemos un resultado: 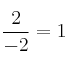
Por tanto: 