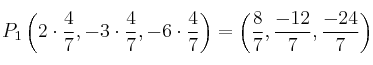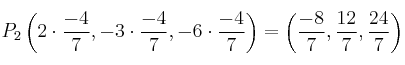Selectividad Andalucía 2009-5-B4

|

Sea la recta r definida por
\left\{ \begin{array}{lll} 3x+2y &=&0 \\3x+z&=&0 \end{array} \right.

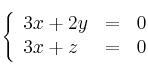
– a) Determine la ecuación del plano perpendicular a r que pasa por el punto P(1,1,1)
– b) Halla los puntos de r cuya distancia al origen es de 4 unidades

SOLUCIÓN

– a) Si el plano es perpendicular a la recta, el vector director de la recta nos valdrá como vector normal del plano.
Dado que tenemos un punto por donde pasa y su vector normal, podemos determinar la ecuación del plano.

En primer lugar hallamos el vector director de la recta (mediante alguno de los procedimientos descritos en los apuntes. Usaremos este: obtenemos un par de puntos de la recta y a partir de ellos el vector director

Si x=0 \longrightarrow y=0 \longrightarrow z=0
El primer punto sería (0,0,0)

Si x=2 \longrightarrow y=-3 (en la 1ª ecuación)
3 \cdot 2 + z=0 \longrightarrow z=-6 (en la 2ª ecuación)
El segundo punto sería (2,-3,-6)

El vector director de la recta será (2,-3,-6), por tanto el plano tendrá como ecuación 2x -3y-6z+D=0

Ahora le hacemos pasar por el punto A(1,1,1) y obtenemos el valor de D
2 \cdot 1 -3 \cdot 1 -6 \cdot 1+D=0
2-3 -6+D=0 \longrightarrow D=7

Ecuación del plano que nos piden: 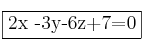\fbox{2x -3y-6z+7=0}

– b) Necesitamos la recta en paramétricas para obtener un punto genérico. Ya tenemos (del apartado a) punto y vector director de la recta, por tanto sus ecuaciones paramétricas son:
\left\{ \begin{array}{lll} x=2 \lambda \\ y=- 3 \lambda \\ z= -6 \lambda \end{array} \right.
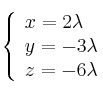
Un punto genérico de la recta es P(2 \lambda, -3 \lambda, -6 \lambda)

La distancia de un punto P al origen O(0,0,0) es el modulo del vector \vec{OP}=(2 \lambda, -3 \lambda, -6 \lambda)

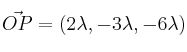
Si la distancia debe ser 4 entonces:
|\vec{OP}|=4
\sqrt{(2 \lambda)^2 + (-3 \lambda)^2 + (-6 \lambda)^2}=4
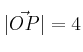
Elevamos al cuadrado para eliminar la raíz
(2 \lambda)^2 + (-3 \lambda)^2 + (-6 \lambda)^2=4^2
4 \lambda^2 + 9 \lambda^2 + 36 \lambda^2=16
49 \lambda^2=16
\lambda^2=\frac{16}{49}
\lambda=\pm \sqrt{\frac{16}{49}} = \pm \frac{4}{7}

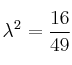
Habría dos puntos que están a 4 unidades de distancia de la recta (uno por cada valor de \lambda obtenido)

P_1 \left(2 \cdot \frac{4}{7}, -3 \cdot \frac{4}{7}, -6 \cdot \frac{4}{7}\right) = \left( \frac{8}{7}, \frac{-12}{7}, \frac{-24}{7}\right)
P_2 \left(2 \cdot \frac{-4}{7}, -3 \cdot \frac{-4}{7}, -6 \cdot \frac{-4}{7}\right) = \left( \frac{-8}{7}, \frac{12}{7}, \frac{24}{7}\right)