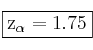Contraste de Hipótesis para la media (unilateral)

Contraste unilateral izquierda

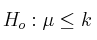$H_o: \mu \leq k$ (hipótesis nula: la media es menor o igual a k)
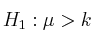$H_1: \mu > k$ (hipótesis alternativa: la media es mayor que k)

Región de aceptación (R)

$R = \left( -\infty, k+Z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}}\right)$

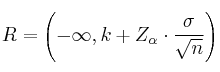
Contraste unilateral derecha

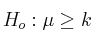$H_o: \mu \geq k$ (hipótesis nula: la media es mayor o igual a k)
$H_1: \mu < k$ (hipótesis alternativa: la media es menor que k)

Región de aceptación (R)

$R = \left( k-Z_{\alpha} \cdot \frac{\sigma}{\sqrt{n}} , +\infty\right)$

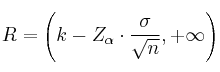
Toma de decisión

– Si 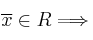$\overline{x} \in R \Longrightarrow$ aceptamos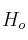
– Si 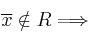$\overline{x} \notin R \Longrightarrow$ rechazamos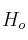

Datos necesarios

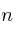– : tamaño de la muestra
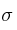– $\sigma$ : desviación típica
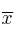– $\overline{x}$ : media de la muestra
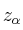– $z_{\alpha}$ : valor crítico

Cálculo del valor crítico 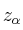$z_{\alpha}$

– Confianza: 90%, 95%, 98%, etc.
– Nivel de confianza: 0.90, 0.95, 0.98, etc.
– Significación+Confianza = 100%

$P(Z \leq z_{\alpha}) = nivel \:confianza$

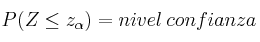
Ejemplo: Confianza del 96%

$P(Z \leq z_{\alpha}) = 0.96$

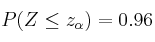
Miramos la tabla de la N(0,1) y vemos que el mas próximo a 0.96 es 0.9599.
Por tanto $\fbox{z_{\alpha}=1.75}$