Integral Definida. Regla de Barrow
La integral definida de un función ![]() entre
entre ![]() y
y ![]() se expresa de la forma
se expresa de la forma 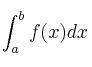 , donde
, donde ![]() y
y ![]() son los límites de integración. Se calcula mediante la Regla de Barrow:
son los límites de integración. Se calcula mediante la Regla de Barrow:
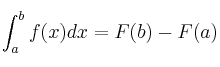
Suponemos que ![]() es una función continua en el intervalo
es una función continua en el intervalo ![]() y
y ![]() es una primitiva de
es una primitiva de ![]() .
.
Para aplicar la Regla de Barrow, calculamos una primitiva ![]() sin constante de integración, y la aplicamos a los limites de integración (calculamos
sin constante de integración, y la aplicamos a los limites de integración (calculamos ![]() y
y ![]() ). Finalmente calculamos la resta
). Finalmente calculamos la resta ![]() .
.
Ejemplo: Calcular la integral definida 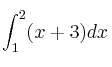
– Primero calculamos la integral indefinida (sin constante):
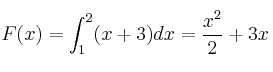
– A continuación aplicamos la Regla de Barrow:
![\int_1^2 (x+3) dx =\left. \frac{x^2}{2} + 3x \right]_1^2 = F(2) - F(1) = \int_1^2 (x+3) dx =\left. \frac{x^2}{2} + 3x \right]_1^2 = F(2) - F(1) =](local/cache-vignettes/L375xH78/cb2e867f809a8b84fcd61c1f8b59c9f7-1a06f.png?1688069388)
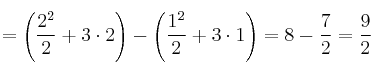
Al calcular una integral definida obtendremos siempre un resultado numérico.
5 - Integral Definida. Aplicaciones de las Integrales
- Secciones
-
MATEMÁTICAS
- 01 - Números Naturales
- 02 - Números Enteros
- 03 - Fracciones
- 04 - Proporcionalidad y Porcentajes
- 05 - Sistemas de medida
- 06 - Polinomios
- 07 - Ecuaciones
- 08 - Sistemas de ecuaciones
- 10 - Sucesiones
- 11 - Geometría en el plano
- 12 - Estadística
- 13 - Probabilidad
- 14 - V.A. Unidimensionales
- 15 - Funciones, Límites y Continuidad
- 16 - Derivadas
- 17 - Integrales
- 18 - Matrices y Determinantes
- 19 - Grafos
- 20 - Geometría en el espacio
- 21 - Trigonometría
- 22 - Logaritmos
- 23 - Matemática Financiera
- 25 - Inferencia Estadística
- LaTeX

