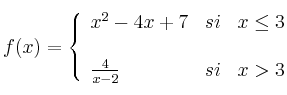Selectividad Andalucía 2004-4-B2

, por dani

|

Continuidad
En (-\infty, 3) es continua (las funciones polinómicas son continuas en todo R)
En (3, +\infty) es continua (es una función racional continua en R-\{-2\}), por tanto es continua en este intervalo, pues el -2 queda fuera del intervalo).
Estudiamos la continuidad en x=3 aplicando la definición de continuidad (por ser un punto de separación entre dos trozos)

– f(3) = 3^2-4 \cdot 3+7 = 4
– \lim\limits_{x \rightarrow 3^-} f(x) = \lim\limits_{x \rightarrow 3} 3x^2-4x+7 = 3^2-4 \cdot 3+7 = 4
\lim\limits_{x \rightarrow 3^+} f(x) = \lim\limits_{x \rightarrow 3} \frac{4}{x-2} = \frac{4}{3-2}= 4
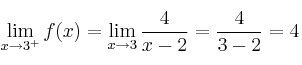
Ambos límites laterales coinciden, por tanto \lim\limits_{x \rightarrow 3} f(x) = 4

Como la imagen y el límite coinciden, podemos afirmar que es continua en x=3

Resumiendo: f(x) es continua en todo R

Derivabilidad

En (-\infty, 3) es derivable y su derivada es 2x-4
En (3, +\infty) es derivable y su derivada es \frac{-4}{(x-2)^2}

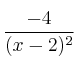
En x=3 debemos comprobar si sus derivadas laterales coinciden:
f\textsc{\char13}(3^-) = 2 \cdot 3 - 4 = 2
f\textsc{\char13}(3^+) = \frac{-4}{(3-2)^2}= -4
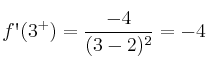
Las derivadas laterales no coinciden, por tanto no es derivable en x=3.

Resumiendo: f es derivable en R - \{3\}, siendo:
f\textsc{\char13}(x)= \left\{ \begin{array}{lcr} 2x-4 & si & x < 3 \\ \\ \frac{-4}{(x-2)^2} & si & x > 3 \\ \end{array} \right.

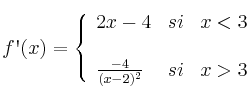
– b) Aplicando la fórmula de la derivada de la función exponencial obtenemos:
f\textsc{\char13}(x)=e^{2x+1} + (x+1) \cdot e^{2x+1} \cdot 2

Aunque no nos piden simplificar, podemos hacerlo sacando factor común e^{2x+1}, y así quedaría:

f\textsc{\char13}(x) = e^{2x+1} \cdot (2x+3)

– Estudie la continuidad y derivabilidad de la función:

f(x)= \left\{ \begin{array}{lcr} x^2-4x+7 & si & x \leq 3 \\ \\ \frac{4}{x-2} & si & x > 3 \\ \end{array} \right.


– Calcule la derivada de g(x)=(x+1) e^{2x+1}