Ejercicios de Mat. Aplicadas C. Sociales I - Funciones
(51) ejercicios de Funciones
-
Indica el tipo de simetrías (si las hay) de las siguientes funciones:
–
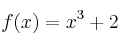
–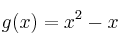
–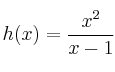
–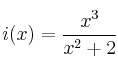
–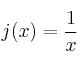
–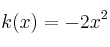
–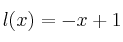
-
Halla los puntos de corte con los ejes de las siguientes funciones:
–
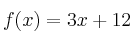
–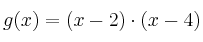
–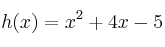
-
Expresa las siguientes funciones mediante forma algebraica:
a) Asignar a cada número real su mitad
b) Asignar a cada número real su raíz cuadrada
c) Asignar a cada número real la mitad de su cuadrado
d) Asignar a cada número real su cubo más cinco -
Indica cuál de las gráficas siguientes representan una función. En caso de ser función, indica su dominio, su imagen y los puntos de corte.
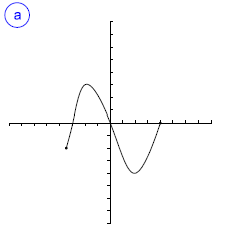 funciones problemas
funciones problemas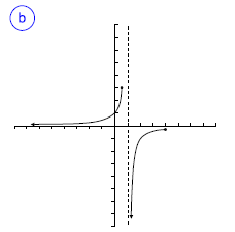 funciones problemas
funciones problemas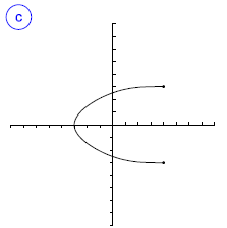 funciones problemas
funciones problemas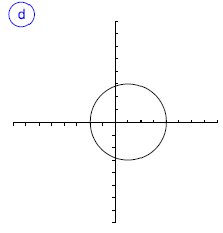 funciones problemas
funciones problemas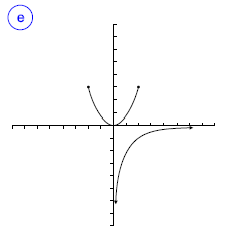 funciones problemas
funciones problemas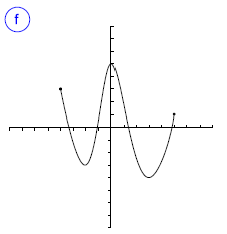 funciones problemas
funciones problemas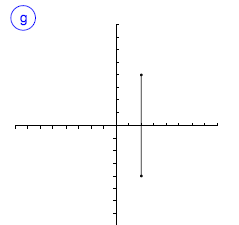 funciones problemas
funciones problemas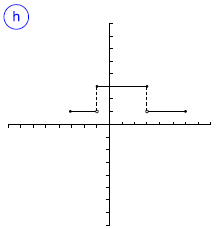 funciones problemas
funciones problemas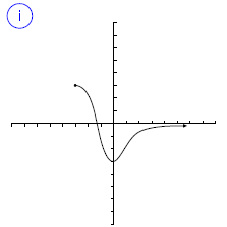 funciones problemas
funciones problemas -
En las siguientes gráficas determina los intervalos de crecimiento y decrecimiento e indica los mínimos o máximos relativos (si los tiene).
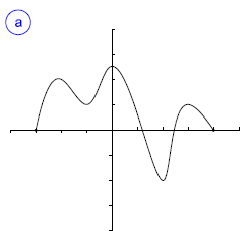 funciones problemas
funciones problemas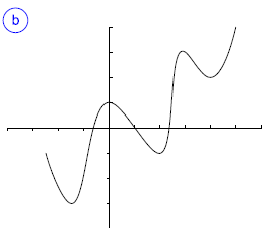 funciones problemas
funciones problemas
 Matemáticas IES
Matemáticas IES
