Ángulo de dos rectas en el espacio 4570

| 2 |

Calcula el ángulo que forman las rectas r y s, siendo sus ecuaciones las siguientes:

r \equiv \frac{x+2}{3} = \frac{y}{-1} = \frac{z-3}{2} \qquad s \equiv \left\{ \begin{array}{l} x=4-3t \\y=-2+t \\z=1+t \end{array}\right.

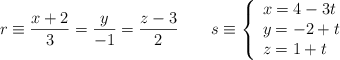
SOLUCIÓN

Para hallar el ángulo entre dos rectas basta con determinar el ángulo que forman sus vectores directores.
Usaremos el producto escalar para determinar el ángulo entre dos vectores

Vector director de r \longrightarrow \vec{u}=(3,-1,2)

Vector director de s \longrightarrow \vec{v}=(-3,1,1)

cos(\widehat{\vec{u},\vec{v}}) = \frac{|\vec{u} \cdot \vec{v}|}{|\vec{u}| \cdot |\vec{v}|} = \frac{|3 \cdot (-3) + (-1) \cdot 1 + 2 \cdot 1|}{\sqrt{3^2+(-1)^2+2^2} \cdot \sqrt{(-3)^2+1^1+1^2}} = \frac{8}{\sqrt{14} \cdot \sqrt{11}}

El ángulo es \alpha = arc \: cos \left( \frac{8}{\sqrt{154}} \right)

Si usamos la calculadora obtendremos aproximadamente 49.86^\circ