Ecuación Vectorial de la Recta
Dada la recta de ecuación vectorial ![]() , se pide:
, se pide:
– tres puntos por los que pase
– tres vectores directores
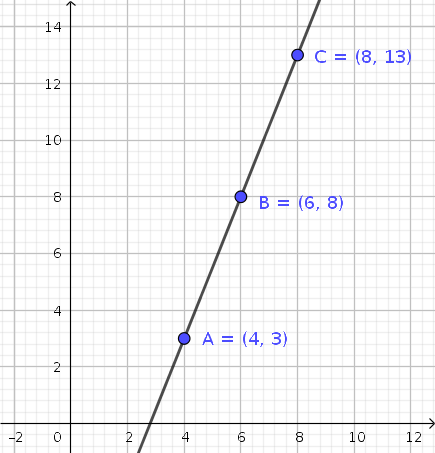
– representación gráfica
SOLUCIÓN
Para obtener puntos de una recta en ecuación vectorial debemos dar valores al parámetro "t" y calcular x,y
Si ![]()
Si ![]()
Si ![]()
Los tres puntos obtenidos son:
![]()
De la ecuación vectorial obtenemos el vector director ![]()
Si queremos más vectores directores basta con conseguir vectores proporcionales:
![]()
![]()
Para representar la recta basta con un par de puntos (usemos los puntos obtenidos en el primer apartado)