Ejercicios de Funciones (I) - 1º Bachillerato de Ciencias
(145) ejercicios de Funciones (I)
-
Estudia gráfica y analíticamente la continuidad de la función:
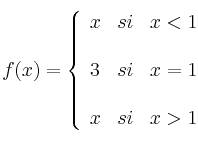
-
Estudia analíticamente la continuidad de la siguiente función en el punto
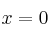 :
:
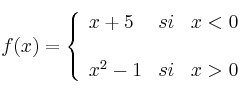
-
Estudia la continuidad en los puntos
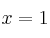 y
y 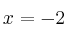 de la función:
de la función:
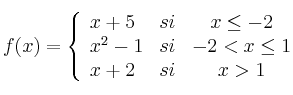
-
Halla el valor de
 para que la siguiente función sea continua:
para que la siguiente función sea continua:
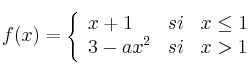
Represente gráficamente la función para el valor de que la hace continua.
que la hace continua.
-
Halla los valores de
 y
y 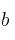 para que la siguiente función sea continua:
para que la siguiente función sea continua:
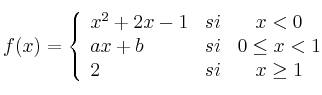
 Matemáticas IES
Matemáticas IES
