Ecuaciones y posiciones relativas de rectas 4198

|

Considera la recta r que pasa por el punto A(1,-2,5) y lleva la dirección del vector \vec{v}=(-2,-2,0)
Se pide:

a) Halla su ecuación paramétrica.

b) Halla su ecuación continua.

c) Halla su ecuación implícita.

d) Estudia la posición relativa de la recta r respecto a la s:
\frac{x-3}{-2}=\frac{y-3}{2}=z-1

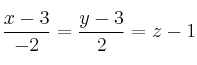
SOLUCIÓN

Ecuaciones paramétricas

\left\{ \begin{array}{lll} x=1 -2 \lambda \\ y=-2-2 \lambda \\ z=5 \end{array} \right.

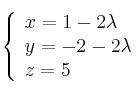
Ecuación continua

\frac{x-1}{-2} = \frac{y+2}{-2} = \frac{z-5}{0}


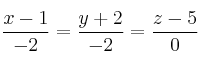
En este caso se dice que la recta no tiene ecuación continua (no se puede dividir por cero)

Ecuaciones implícitas
\frac{x-1}{-2}=\frac{y+2}{-2}
\frac{x-1}{-2} = \frac{z-5}{0}

\left\{ \begin{array}{lll} (-2)(x-1)=(-2)(y+2) \\ (x-1) \cdot 0 = (-2)(z-5) \end{array} \right.

\left\{ \begin{array}{lll} -2x+2=-2y-4 \\ 0 = -2z+10 \end{array} \right.

\left\{ \begin{array}{lll} -2x+2y+6 = 0 \\ -2z+10 = 0 \end{array} \right.

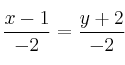
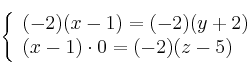
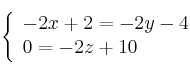
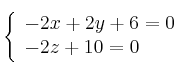
Para estudiar la posición relativa de dos rectas en el espacio Ver Teoría necesitamos un vector director de cada recta y un tercer vector formado por un punto de cada recta

\vec{v_r}=(-2,-2,0)
\vec{v_s}=(-2,2,1)
P_r \rightarrow A(1,-2,5)
P_s \rightarrow B(3,3,1)
\vec{AB}=(2,5,-4)

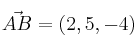
Analizamos el rango de la matriz formada por los tres vectores

M = \left( \begin{array}{ccc} -2 & -2 & 0 \\ -2 & 2 & 1 \\ 2 & 5 & -4 \end{array} \right)

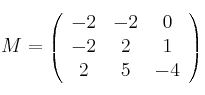
|M| =38 \neq 0 \rightarrow rg(A)=3 \rightarrowlas rectas se cruzan