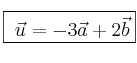Ej 1 de Combinación Lineal
Expresa el vector ![]() como combinación lineal de los vectores
como combinación lineal de los vectores ![]() y
y 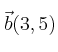
SOLUCIÓN
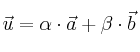
![]()
![]()
![]()
![]()
Si igualamos componente a componente obtendremos un sistema de dos ecuaciones con dos incógnitas:
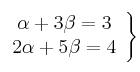
Resolvemos el sistema por sustitución:
Despejamos en la primera ecuación
Y sustituimos en la segunda
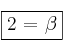
![]()
![]()
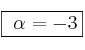
Por tanto, a combinación lineal que nos piden es: