Ej 2 de Continuidad

|

Estudia analíticamente la continuidad de la siguiente función en el punto x=0:

f(x)= \left\{ \begin{array}{lcc} x+5 & si & x < 0 \\ \\ x^2-1 & si & x >0 \end{array} \right.

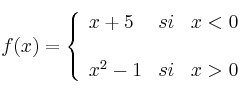
SOLUCIÓN

La función es continua en (-\infty, 0) y en (0,+\infty) por ser polinómica en ambos (las funciones polinómicas son siempre continuas).

Para el punto x=0 (punto que separa ambos trozos) debemos aplicar la definición de continuidad en un punto: Debe existir la imagen en ese punto, deben existir ambos límites laterales de dicho punto y además la imagen debe coincidir con el límite.

Como no existe f(0), ya no se cumple la primera condición de continuidad. Entonces no es necesario mirar los límites laterales, y podemos afirmar que No es continua en x=0