Ej 4 de Continuidad

|

Halla el valor de a para que la siguiente función sea continua:

f(x)= \left\{ \begin{array}{lcc} x+1 & si & x \leq 1 \\ 3-ax^2 & si & x> 1 \end{array} \right.


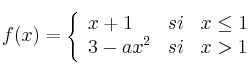
Represente gráficamente la función para el valor de a que la hace continua.

SOLUCIÓN

- En (-\infty , 1) es continua por ser polinómica
- En (1, +\infty) es continua por ser polinómica
- Veamos qué ocurre en x=1.
como el 1 es un punto de separación entre los dos trozos de la función, debemos aplicar la definición de continuidad.
f(1) = 1+1 = 2
\lim\limits_{x \rightarrow 1^-} \: f(x) = \lim\limits_{x \rightarrow 1} \: x+1 = 1+1 = 2
\lim\limits_{x \rightarrow 1^+} \: f(x) = \lim\limits_{x \rightarrow 1} \: 3-ax^2 = 3-a
Para que sea continua en x=1 tienen que coincidir ambos límites laterales, y además deben ser igual a f(1); por tanto:
3-a = 2 de donde \fbox{a=1}

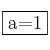
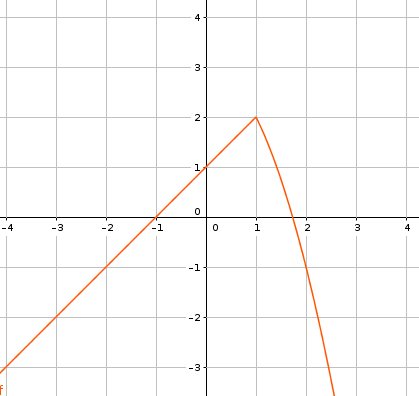
Gráfica de la función: