Ejercicio vectores 3 dimensiones

|

Dados los vectores \vec{u}=(2,-1,5) , \vec{v}=(1,-8,7) y \vec{w}=(1,1,0) , se pide:

– a) ¿Son linealmente dependientes los 3 vectores?
– b) Calula \vec{u} \times \vec{w} (producto vectorial)
– c) Encuentra dos vectores paralelos al vector \vec{u}
– d) Encuentra dos vectores perpendiculares al vector \vec{u}
– e) Halla el ángulo que forman los vectores \vec{u} y \vec{v}

SOLUCIÓN

– a) ¿Son linealmente dependientes los 3 vectores?
\left| \begin{array}{ccc} 2 & -1 & 5 \\ 1 & -8 & 7 \\ 1 & 1 & 0 \end{array} \right| = 24
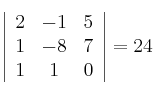
Como el determinante es distinto de cero, los vectores son linealmente independientes

– b) Calula \vec{u} \times \vec{w} (producto vectorial)
\vec{u} \times \vec{w}= \left| \begin{array}{ccc} \vec{i} &\vec{j} &\vec{k} \\ 2 & -1 & 5 \\ 1 & 1 & 0 \end{array} \right| = -5\vec{i}+5\vec{j}+3\vec{k}

Por tanto \vec{u} \times \vec{w} = (-5,5,3)

– c) Encuentra dos vectores paralelos al vector \vec{u}
Para encontrar vectores paralelos, basta con crear vectores proporcionales, por ejemplo (4,-2,10) , (6,-3,15)

– d) Encuentra dos vectores perpendiculares al vector \vec{u}
(1,2,0) , (2,4,0)

– e) Halla el ángulo que forman los vectores \vec{u} y \vec{v}

La fórmula del producto escalar

\vec{u} \cdot \vec{v} = |\vec{u}| \cdot |\vec{v}| \cdot cos(\widehat{\vec{u},\vec{v}})


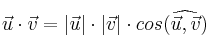
nos permite averiguar el ángulo que forman dos vectores, despejando el coseno:

cos(\widehat{\vec{u},\vec{v}})=\frac{\vec{u} \cdot \vec{v}}{|\vec{u}| \cdot |\vec{v}|}

cos(\alpha)=\frac{\vec{u} \cdot \vec{v}}{|\vec{u}| \cdot |\vec{v}|}


cos(\alpha)=\frac{2 \cdot 1 + (-1) \cdot (-8) + 5 \cdot 7}{\sqrt{2^2+(-1)^2+5^2} \cdot \sqrt{1^2+(-8)^2+7^2}}


cos(\alpha)=\frac{45}{\sqrt{30} \cdot \sqrt{114}} = \frac{45}{ \sqrt{3420}}

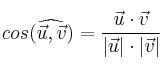
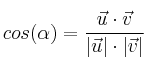
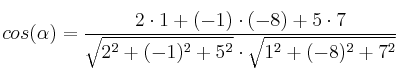
Usamos la calculadora y vemos que el ángulo es aproximadamente 39.7 grados