Funciones Asíntotas

Halla las asíntotas de la función:
$y = \frac{x^3}{2x^2-8}$

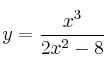
SOLUCIÓN

$y = \frac{x^3}{2x^2-8}$

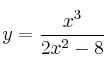
Asíntotas verticales

Las buscamos entre los valores que anulan el denominador
$2x^2-8=0 \longrightarrow 2x^2=8 \longrightarrow x^2=4 \longrightarrow x=\pm2$

$\lim_{x \rightarrow 2} \frac{x^3}{2x^2-8} = \frac{2^3}{2 \cdot 2^2-8}=\frac{8}{0} \longrightarrow \infty \Rightarrow A.V. \:\: \textcolor{blue}{x=2}$

$\lim_{x \rightarrow -2} \frac{x^3}{2x^2-8} = \frac{(-2)^3}{2 \cdot (-2)^2-8}=\frac{-8}{0} \longrightarrow \infty \Rightarrow A.V. \:\: \textcolor{blue}{x=-2}$

Veamos el comportamiento de la función respecto a las asíntotas. Para ello estudiamos los límites laterales

$\lim_{x \rightarrow 2^-} \frac{x^3}{2x^2-8} = \frac{2^3}{0^-}=-\infty$
$\lim_{x \rightarrow 2^+} \frac{x^3}{2x^2-8} = \frac{2^3}{0^+}=+\infty$

$\lim_{x \rightarrow -2^-} \frac{x^3}{2x^2-8} = \frac{(-2)^3}{0^+}=-\infty$
$\lim_{x \rightarrow -2^+} \frac{x^3}{2x^2-8} = \frac{(-2)^3}{0^-}=+\infty$

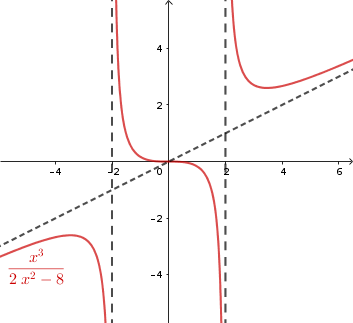
En la siguiente gráfica se puede ver el comportamiento de la función respecto de sus asíntotas

Asíntotas horizontales

$\lim_{x \rightarrow \infty} \frac{x^3}{2x^2-8} = \infty$

Al ser el grado del numerador mayor, el límite es infinito, por tanto no hay asíntotas horizontales

Asíntotas oblicuas

La asíntota oblicua es suna recta de ecuación , donde m y n vienen dadas por las expresiones siguientes:

$m = \lim\limits_{x \rightarrow \infty} \frac{f(x)}{x}$
$n = \lim\limits_{x \rightarrow \infty} \left[f(x) -mx\right]$

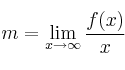
En nuestro caso sería:

$m = \lim\limits_{x \rightarrow \infty}\left( \frac{x^3}{2x^2-8} : x \right)=\lim\limits_{x \rightarrow \infty} \frac{x^3}{2x^3-8x}= \frac{1}{2}$

$n = \lim\limits_{x \rightarrow \infty} \left[\frac{x^3}{2x^2-8} -\frac{1}{2}x\right]=\lim\limits_{x \rightarrow \infty} \left[\frac{2x^3-x \cdot (2x^2-8)}{2 \cdot (2x^2-8)} \right]=$
$= \lim\limits_{x \rightarrow \infty}\frac{8x}{4x^2-16} = 0$
El límite vale 0 porque el grado del denominador es mayor