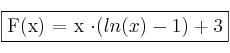Integral de Logaritmo Neperiano
Dada la función ![]() , calcula una primitiva de
, calcula una primitiva de ![]() cuya gráfica pase por el punto
cuya gráfica pase por el punto ![]()
SOLUCIÓN
Calculamos 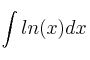 por partes:
por partes:
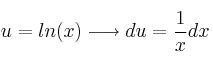
![]()
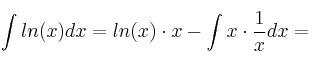
![]()
Por tanto, cualquier primitiva será de la forma:
![]()
La primitiva que pasa por (e,3) cumple que F(e) = 3
![]()
![]()
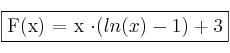
Dada la función ![]() , calcula una primitiva de
, calcula una primitiva de ![]() cuya gráfica pase por el punto
cuya gráfica pase por el punto ![]()
Calculamos 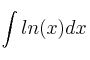 por partes:
por partes:
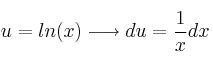
![]()
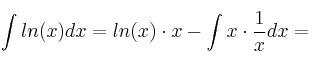
![]()
Por tanto, cualquier primitiva será de la forma:
![]()
La primitiva que pasa por (e,3) cumple que F(e) = 3
![]()
![]()