Monotonía y extremos
Estudia monotonía y extremos en la función ![]()
SOLUCIÓN
Para estudiar los intervalos de crecimiento y decrecimiento seguimos el procedimiento descrito en la teoría.
![]()

Los intervalos a considerar serían:

Tomamos un punto de cada intervalo y le aplicamos la derivada (si da positivo crece, y si da negativo decrece)
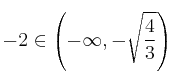
![]() DECRECE
DECRECE
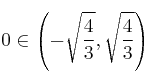
![]() CRECE
CRECE
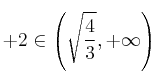
![]() DECRECE
DECRECE
Extremos
Dado que es una función continua (es polinómica) podemos obtener los extremos a partir del estudio hecho para la monotonía.
Si CRECE en 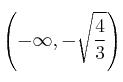 y DECRECE en
y DECRECE en 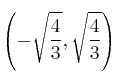 al ser continua tiene un máximo en
al ser continua tiene un máximo en 
Razonando de forma semejante vemos que tiene un mínimo en 