Matemáticas IES
Perpendicular por el punto medio de segmento
y 
, halla la ecuación paramétrica de la recta perpendicular al segmento 
en su punto medio. SOLUCIÓN
La recta que nos piden tiene como vector director cualquier vector perpendicular a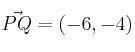 
, por ejemplo 
.
[Para obtener un vector perpendicular a uno dado, basta con cambiar de orden las componentes y a una de ellas cambiarle el signo)
Como punto, debemos tomar el punto medio de 
, que será: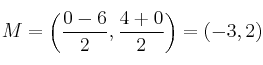 
Punto medio de un segmento
Por tanto, las ecuaciones paramétricas de la recta 
que nos piden son:
