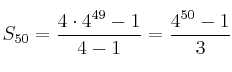Problema de sucesiones 4211

|

Inventa una sucesión aritmética y otra geométrica cuyo primer término sea 1 y el segundo 4. Escribe los 10 primeros términos de cada una , el término general y la suma de los 50 primeros.

SOLUCIÓN

Progresión aritmética, tal que a_1 = 1 , a_2=4

La diferencia es d=3

Los 10 primeros términos:
1 , 4 , 7 , 10 , 13 , 16 , 19 , 22 , 25 , 28

Término general: a_n=a_1+(n-1)\cdot d
En nuestro caso será: a_n=1+(n-1)\cdot 3
Operando tendremos: a_n=3n-2

Para la suma de los 50 primeros términos usamos la fórmula
S_n=\frac{(a_1+a_n) \cdot n}{2}
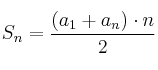
que en nuestro caso resulta en:
S_{50}=\frac{(a_1+a_{50}) \cdot 50}{2}
a_1=1
a_{50}=3 \cdot 50 - 2 = 148
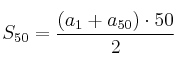
Entonces 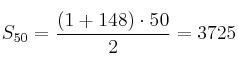S_{50}=\frac{(1+148) \cdot 50}{2}= 3725

Progresión geométrica, tal que a_1 = 1 , a_2=4

La razón es r=4

Los 10 primeros términos:
1 , 4 , 16 , 64 , 256 , 1024 , 4096 , 16384 , 65536 , 262144

Término general: a_n=a_1 \cdot r^{n-1} }
En nuestro caso será: a_n=1 \cdot 4^{n-1}}
Es decir, sería: a_n=4^{n-1}}

Para la suma de los 50 primeros términos usamos la fórmula
S_n=\frac{r \cdot a_n - a_1 }{r-1}

que en nuestro caso resulta en:
S_{50}=\frac{4 \cdot a_{50} - a_1 }{4-1}

a_1=1
a_{50}=4^{50-1} = 4^{49}
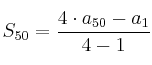
Entonces S_{50}=\frac{4 \cdot 4^{49} - 1 }{4-1}=\frac{4^{50} - 1 }{3}