Problema progresiones 4543

|

Encuentre el número de términos que se deben sumar de la progresión aritmética 9, 11, 13,... para que la suma sea igual a la de los nueve primeros términos de la progresión geométrica 3, -6, 12, -24,...

SOLUCIÓN

En las progresiones geométricas el término general responde a la fórmula a_n=a_1 \cdot r^{n-1} y la suma de los n primeros términos es S_n=\frac{r \cdot a_n - a_1 }{r-1}

En el caso de 3, -6, 12, -24,.. la razón es r=-2

Entonces a_n=3 \cdot (-2)^{n-1}

a_9=3 \cdot (-2)^{9-1} = 3 \cdot (-2)^8 = 3 \cdot 2^8 = 768

S_9=\frac{(-2) \cdot a_9 - a_1 }{(-2)-1} = \frac{(-2) \cdot 768 - 3 }{-3} = 513

Por tanto, la suma de los 9 primeros términos es 513

Ahora en la progresión aritmética debemos calcular el número de términos necesarios para que su suma sea 513

En la progresión aritmética 9, 11, 13, .. la diferencia es d=2 y el término general es

a_n=a_1+(n-1)\cdot d
a_n= 9 + (n-1) \cdot 2 = 9+2n-2 = 2n+7

La suma de los n primeros términos es

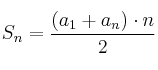S_n=\frac{(a_1+a_n) \cdot n}{2} (que debe valer 513)

513=\frac{(9+a_n) \cdot n}{2}

Sustituimos a_n por 2n+7

513=\frac{(9+2n+7) \cdot n}{2}

513=\frac{(2n+16) \cdot n}{2}

513 \cdot 2= 2n^2+16n

2n^2+16n-1026=0 (podemos simplificar antes de resolver)
n^2+8n-513=0
Resolvemos la ecuación de segundo grado y obtenemos como soluciones 19 y -27
Descartamos la negativa pues "n" tiene que ser un número Natural.

Por tanto la solución es 19 términos.