Recta tangente a función
Calcula el valor de ![]() para que la recta
para que la recta ![]() sea tangente a la curva
sea tangente a la curva ![]()
SOLUCIÓN
– Una recta ![]() tiene de pendiente
tiene de pendiente ![]() , por tanto la recta
, por tanto la recta ![]() tiene por pendiente
tiene por pendiente ![]() .
.
– Sabemos por otra parte, que la pendiente de la recta tangente es la derivada, por tanto l, para que sea tangente, la derivada debe valer ![]() en algún punto:
en algún punto:
![]()
Es decir, será tangente en el punto de abcisa ![]() .
.
Ahora podemos seguir varios razonamientos:
– Método 1: Hallamos la ecuación de la recta tangente en $x=1$ aplicando la fórmula:
![]()
![]()
Como la tg es ![]() tenemos que
tenemos que 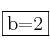
– Método 2: En ![]() hay un punto de tangencia, lo que quiere decir que su imagen será la misma por la función que por la recta (al ser tangencia coinciden).
hay un punto de tangencia, lo que quiere decir que su imagen será la misma por la función que por la recta (al ser tangencia coinciden).
