SOLUCIÓN

Hay dos posibles dibujos del triángulo

Si trazamos la altura, el triángulo queda dividido en dos triángulos rectángulos iguales (siempre debemos buscar triángulos rectángulos para poder aplicar Pitágoras y las razones trigonométricas)

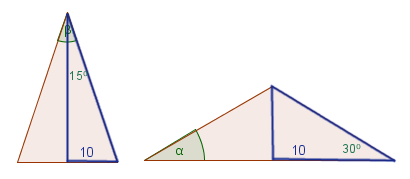
Recordemos que resolver un triángulo es hallar el valor de todos sus ángulos y de todos sus lados. Lo haremos para ambos casos

Primer caso
– Un ángulo (el desigual) vale 30⁰
– Entre los otros dos ángulos tienen que sumar 180-30 = 150⁰ (porque entre los 3 ángulos de cualquier triangulo deben sumar 180⁰)
– Por tanto los otros dos ángulos miden 75⁰ cada uno

Si nos fijamos en el triángulo rectángulo de la derecha y llamamos a uno de los lados iguales, podemos aplicar las razones trigonométricas:

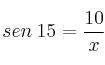, de donde aprox.

Por tanto los lados iguales miden 38.6 y el desigual 20

Segundo caso
En el segundo dibujo los ángulos valen 30, 30 y 120

Si miramos el triángulo rectángulo remarcado y llamamos a la hipotenusa, podemos expresar:
, de donde:
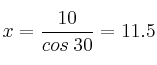aproximadamente.

Por tanto los lados iguales valen aprox. 11.5 y el lado desigual 20