Selectividad Andalucía 2014 - 1 - B2

|

Sea f : R \longrightarrow R la función definida por f(x) = e^x \cdot cos(x)

– a) Calcula la ecuación de la recta tangente a la gráfica de f en el punto de abcisa x=0
– b) Calcula la primitiva de f cuya gráfica pasa por el punto (0,0)

SOLUCIÓN

– a) La ecuación de la recta tangente (ver teoría) en el punto de abcisa x=a viene dada por la expresión
y-f(a) = f\textsc{\char13}(a) \cdot (x-a)
Para el punto x=0 sería:
y-f(0) = f\textsc{\char13}(0) \cdot (x-0)

Necesitamos calcular f(0) y f\textsc{\char13}(0)

f(0)=e^0 \cdot cos(0) = 1 \cdot 1 = 1
f\textsc{\char13}(x)=e^x \cdot cos(x) + e^x \cdot (-sen(x))
f\textsc{\char13}(0)=e^0 \cdot cos(0) + e^0 \cdot (-sen(0))= 1 \cdot 1 + 1 \cdot 0=1
Por tanto la recta quedaría así y-1 = 1 \cdot (x-0)
Que podemos expresar como 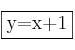\fbox{y=x+1}

– b) Debemos calcular la integral indefinida con constante de integración, que es el conjunto de todas las primitivas de la función. Después le hacemos cumplir la condición de que pase por (0,0) y eso nos dará el valor de la constante.

Para calcular 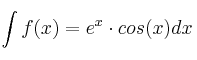\int f(x) = e^x \cdot cos(x) dx usaremos el método de integración por partes, llamando «u» a la trigonométrica y «dv» a la exponencial (a las exponenciales siempre les asignamos «dv» porque son más fáciles de integrar).
u = cosx \longrightarrow du=-senx \: dx
dv = e^x \longrightarrow v=\int e^x dx = e^x
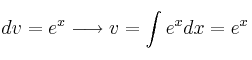
Aplicamos la fórmula 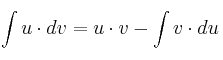\int u \cdot dv = u \cdot v - \int v \cdot du y obtenemos:
\int e^x \cdot cos(x) dx = cosx \cdot e^x - \int e^x (-senx)dx
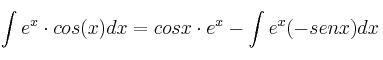
que podemos expresar de la forma:
\int e^x \cdot cos(x) dx = e^x cosx+ \int e^x senx \: dx

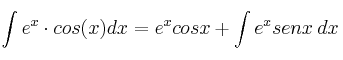
Volvemos a aplicar "partes" a 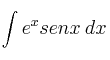\int e^x senx \: dx
u = senx \longrightarrow du=cosx \: dx
dv = e^x \longrightarrow v=\int e^x dx = e^x
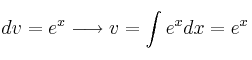
Aplicando la fórmula de integración por partes:
\int e^x senx \: dx = senx \cdot e^x - \int e^x cosx \: dx

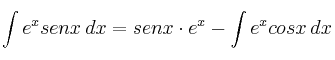
En definitiva tendríamos:
\int e^x cosx dx = e^x cosx+ senx \cdot e^x - \int e^x cosx \: dx
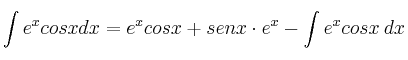
Si llamamos 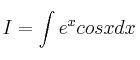I = \int e^x cosx dx, podemos expresarlo así:

I = e^x \: cosx+ e^x senx - I


2I = e^x cosx+ e^x senx


I = \frac{e^x cosx+ e^x senx}{2}

\int e^x cosx \: dx= \frac{e^x cosx+ e^x senx}{2}

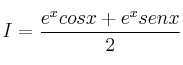
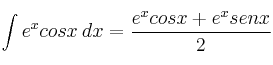
Por tanto, cualquier primitiva será de la forma:
F(x) = \frac{e^x cosx+ e^x senx}{2} + C

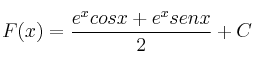
Para calcular la que pasa por (0,0) , basta con aplicar F(0)=0
F(0) = 0 \longrightarrow \frac{e^0 cos(0) + e^0 sen(0)}{2} + C =0
\frac{1}{2}+C=0 \longrightarrow C = -\frac{1}{2}

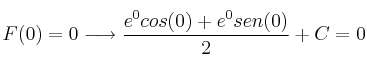
La primitiva que nos piden sería:
F(x) = \frac{e^x cosx+ e^x senx}{2} - \frac{1}{2}