Sistema 2x2 No Lineal

Resuelve el sistema de ecuaciones:
$\left\{ \begin{array}{ll} (x+y) \cdot (x-y) = 7 \\ 3x - 4y = 0 \end{array} \right.$

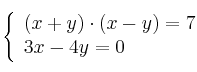
SOLUCIÓN

$\left\{ \begin{array}{ll} (x+y) \cdot (x-y) = 7 \\ 3x - 4y = 0 \end{array} \right.$

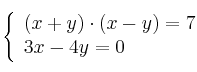
Los sistemas no lineales se suelen resolver por sustitución

Despejamos "x" en la segunda ecuación

$3x-4y=0 \longrightarrow 3x=4y \longrightarrow \textcolor{blue}{x=\frac{4y}{3}}$

Ahora sustituimos en la primera ecuación

$(x+y) \cdot (x-y) = 7$

$\left(\frac{4y}{3}+y\right) \cdot \left(\frac{4y}{3}-y\right) = 7$

$\frac{7y}{3} \cdot \frac{y}{3} = 7$

$\frac{7y^2}{9} = 7$

$\frac{7y^2}{9} = 9 \cdot 7$

$7y^2 = 9 \longrightarrow \textcolor{blue}{y = \pm 3}$

– Si $\textcolor{red}{y=3} \longrightarrow x = \frac{4 \cdot 3}{3} \longrightarrow \textcolor{red}{x =4}$

– Si $\textcolor{red}{y=-3} \longrightarrow x = \frac{4 \cdot (-3)}{3} \longrightarrow \textcolor{red}{x =-4}$

El sistema tiene dos soluciones:

$\fbox{x=4 \: ; \: y=3} \quad , \quad \fbox{\quad x=-4 \: ; \:y=-3 }$