fracciones algebraicas

Opera y simplifica:
$\frac{3x}{x^2-4} - \frac{2}{x-2} - \frac{x-3}{x^2+4x+4}$

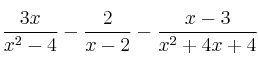
SOLUCIÓN

1) Factorizamos los denominadores. Para ello debemos recordar las fórmulas de los productos notables

$\frac{3x}{(x+2)(x-2)} - \frac{2}{x-2} - \frac{x-3}{(x+2)^2}$

2) Calculamos m.c.m. de los denominadores

$m.c.m. \Big( (x+2)(x-2) , (x-2) , (x+2)^2 \Big)= (x-2) \cdot (x+2)^2$

3) Reducimos las fracciones a común denominador

$\frac{}{(x-2)(x+2)^2} - \frac{}{(x-2)(x+2)^2} - \frac{}{(x-2)(x+2)^2}$

$\frac{(x+2) \cdot 3x}{(x-2)(x+2)^2} - \frac{(x+2)^2 \cdot 2}{(x-2)(x+2)^2} - \frac{(x-2) \cdot (x-3)}{(x-2)(x+2)^2}=$

$\frac{(x+2) \cdot 3x - (x+2)^2 \cdot 2 - (x-2) \cdot (x-3)}{(x-2)(x+2)^2} =$

$\frac{3x-14}{(x-2)(x+2)^2}$