Encontrados 10 ejercicios del examen de
UNED Junio 2012 Modelo M
-
(#3393) - UNED A25 - 2012 Junio M 01

El dominio de la función
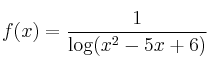 es:
es:– A)
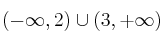
– B)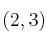
– C)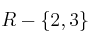
-
(#3394) - UNED A25 - 2012 Junio M 02

La gráfica de la función
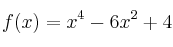 en
en 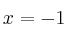 tiene:
tiene:– A) Punto de inflexión.
– B) Máximo.
– C) Mínimo. -
(#3395) - UNED A25 - 2012 Junio M 03

Una ecuación de la recta que pasa por el punto
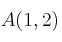 y es perpendicular a
y es perpendicular a 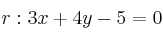 es:
es:– A)
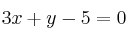
– B)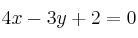
– C)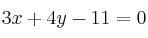
-
(#3396) - UNED A25 - 2012 Junio M 04

El sistema
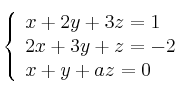 es:
es:– A) Incompatible si
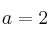
– B) Compatible determinado si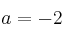
– C) Compatible determinado si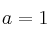
-
(#3397) - UNED A25 - 2012 Junio M 05

El valor de
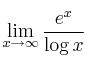 es:
es:– A) 0
– B) 1
– c)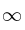
-
(#3398) - UNED A25 - 2012 Junio M 06

Los vectores
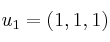 ,
, 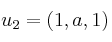 y
y 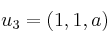 verifican que:
verifican que:– A) Forman una base para
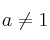
– B) Son linealmente dependientes para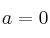
– C)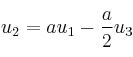
-
(#3399) - UNED A25 - 2012 Junio M 07

La función
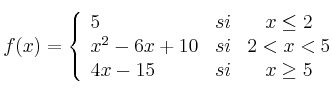 es:
es:– A) Continua en
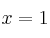
– B) Discontinua en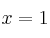
– C) Discontinua en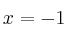
-
(#3400) - UNED A25 - 2012 Junio M 08

De cuántas maneras distintas se pueden ordenar las letras de la palabra CURSO:
– A) 150
– B) 120
– C) 100 -
(#3401) - UNED A25 - 2012 Junio M 09

El valor de la integral
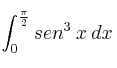 es:
es:– A)
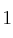
– B)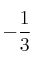
– C)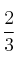
Indicación:
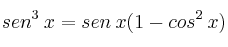
-
(#3402) - UNED A25 - 2012 Junio M 10

La derivada de la función
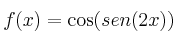 es:
es:– A)
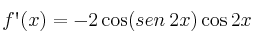
– B)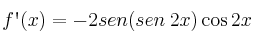
– C)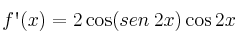
 Matemáticas IES
Matemáticas IES
