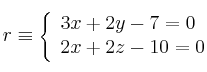-
Halla la ecuación del plano que pasa por los puntos 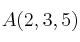 ,
, 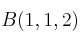 y
y 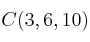
-
Halla dos puntos y dos vectores directores de la recta
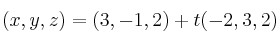
-
Halla dos puntos y dos vectores directores de la recta
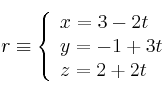
-
Halla dos puntos y dos vectores directores de la recta
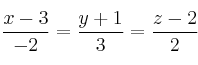
-
Halla dos puntos y dos vectores directores de la recta