Expresión matricial de un sistema lineal
Dado un sistema de ecuaciones
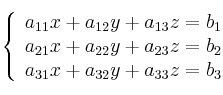
Se puede expresar de forma matricial de la siguiente manera:
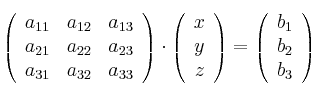
La expresión anterior, de forma abreviada ![]() , se llama expresión matricial del sistema. Las matrices se conocen como:
, se llama expresión matricial del sistema. Las matrices se conocen como:
– ![]() matriz de los coeficientes
matriz de los coeficientes
– ![]() matriz de las incógnitas
matriz de las incógnitas
– ![]() matriz de los términos independientes
matriz de los términos independientes
Matriz ampliada
Se llama matriz ampliada (se representa por ![]() ) a la matriz de los coeficientes ampliada con la columna de los términos independientes.
) a la matriz de los coeficientes ampliada con la columna de los términos independientes.
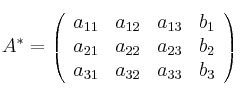
Es frecuente expresar la matriz de los coeficientes (![]() ) y la matriz ampliada (
) y la matriz ampliada (![]() ) en una única expresión:
) en una única expresión:

 Matemáticas IES
Matemáticas IES
