-
a) Dadas las inecuaciones
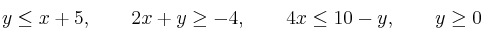
represente el recinto que limitan y calcule sus vértices.
b) (0.7 puntos) Obtenga el máximo y el mínimo de la función 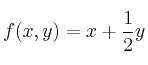 en el recinto anterior, así como los puntos en los que se alcanzan.
en el recinto anterior, así como los puntos en los que se alcanzan.
-
La concejalía de Educación de una determinada localidad afirma que el tiempo medio dedicado a la lectura por los jóvenes de entre 15 y 20 años de edad es, a lo sumo, de 8 horas semanales. Para contrastar esta hipótesis, (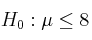 ) se escoge al azar una muestra de 100 jóvenes, de entre 15 y 20 años, y se obtiene una media de 8.3 horas de dedicación a la lectura. Supuesto que el tiempo dedicado a la lectura sigue una ley Normal con desviación típica igual a 1 hora, ¿qué se puede decir, a un nivel de significación del 5%, sobre la afirmación de la concejalía?
) se escoge al azar una muestra de 100 jóvenes, de entre 15 y 20 años, y se obtiene una media de 8.3 horas de dedicación a la lectura. Supuesto que el tiempo dedicado a la lectura sigue una ley Normal con desviación típica igual a 1 hora, ¿qué se puede decir, a un nivel de significación del 5%, sobre la afirmación de la concejalía?
-
En un servicio técnico especializado en cámaras fotográficas, el  de las cámaras que se reciben son del modelo A y el resto del modelo B. El
de las cámaras que se reciben son del modelo A y el resto del modelo B. El 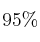 de las cámaras del modelo A son reparadas, mientras que del modelo B sólo se reparan el
de las cámaras del modelo A son reparadas, mientras que del modelo B sólo se reparan el 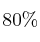 . Si se elige una cámara al azar:
. Si se elige una cámara al azar:
– a) Calcule la probabilidad de que no se haya podido reparar.
– b) Si se observa que no ha sido reparada, ¿cuál es la probabilidad de que sea del modelo B?
-
Un estudio estadístico de la producción de una fábrica de batidoras determina que el 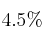 de las batidoras presenta defectos eléctricos, el
de las batidoras presenta defectos eléctricos, el 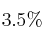 presenta defectos mecánicos y el
presenta defectos mecánicos y el 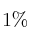 presenta ambos defectos. Se escoge al azar una batidora.
presenta ambos defectos. Se escoge al azar una batidora.
– a) Calcule la probabilidad de que no tenga ninguno de los dos defectos.
– b) Calcule la probabilidad de que tenga un defecto mecánico sabiendo que tiene un defecto eléctrico.
– c) Justifique si los sucesos “tener un defecto eléctrico” y “tener un defecto mecánico” son independientes. ¿Son incompatibles?
-
Sean A y B dos sucesos aleatorios independientes de los que se conoce que:
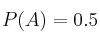 y
y 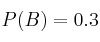
– a) Diga, razonadamente, si A y B son sucesos incompatibles.
– b) ¿Cuál es la probabilidad de que suceda A y no suceda B?
– c) Calcule 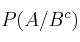
 andalucía
andalucía aragón
aragón asturias
asturias cantabria
cantabria castilla_leon
castilla_leon castilla_mancha
castilla_mancha catalunya
catalunya madrid
madrid MatemáticasII_Andalucía_2001
MatemáticasII_Andalucía_2001 MatemáticasII_Andalucía_2002
MatemáticasII_Andalucía_2002 MatemáticasII_Andalucía_2003
MatemáticasII_Andalucía_2003 MatemáticasII_Andalucía_2004
MatemáticasII_Andalucía_2004 MatemáticasII_Andalucía_2005
MatemáticasII_Andalucía_2005 MatemáticasII_Andalucía_2006
MatemáticasII_Andalucía_2006 MatemáticasII_Andalucía_2007
MatemáticasII_Andalucía_2007 MatemáticasII_Andalucía_2008
MatemáticasII_Andalucía_2008 MatemáticasII_Andalucía_2009
MatemáticasII_Andalucía_2009 MatemáticasII_Andalucía_2010
MatemáticasII_Andalucía_2010 MatematicasII_Andalucía_2011
MatematicasII_Andalucía_2011 MatemáticasII_Andalucía_2012
MatemáticasII_Andalucía_2012 Matemáticas IES
Matemáticas IES
 Matemat_Soc_Andalucia_2014
Matemat_Soc_Andalucia_2014