Distancia entre rectas que se cruzan

|

Halla la distancia entre las rectas:
r \equiv \frac{x+3}{3}=\frac{y-9}{-2} = \frac{z-8}{-2}
s \equiv \frac{x-3}{-2}=\frac{y-2}{1} = \frac{z-1}{2}

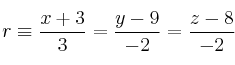
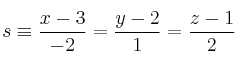
SOLUCIÓN

En primer lugar estudiamos la posición relativa de las rectas siguiendo este método
Necesitaremos un punto y un vector de cada recta

r \equiv \frac{x+3}{3}=\frac{y-9}{-2} = \frac{z-8}{-2}

\vect{v_r} = (3, -2, -2)

P_r (-3, 9, 8)

s \equiv \frac{x-3}{-2}=\frac{y-2}{1} = \frac{z-1}{2}

\vect{v_s} = (-2, 1, 2)

P_s(3, 2, 1)

\vect{P_rP_s} = (6,-7,-7)

M = \left( \begin{array}{ccc} 3 & -2 & -2 \\ -2 & 1 & 2 \\ 6 & -7 & -7 \end{array} \right)

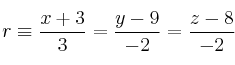
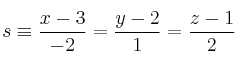
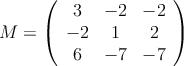
det(M)=9 \longrightarrow r y s se cruzan

Ahora calculamos la distancia siguiendo el método 3 de la teoría

d(r,s) = \frac{\left| [\vec{v_r},\vec{v_s},\vec{P_rP_s}] \right|}{\left| \vec{v_r} \times \vec{v_s} \right|}

[\vec{v_r},\vec{v_s},\vec{P_rP_s}] = \left| \begin{array}{ccc} 3 & -2 & -2 \\ -2 & 1 & 2 \\ 6 & -7 & -7 \end{array} \right| = 9

\vec{v_r} \times \vec{v_s} = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 3 & -2 & -2 \\ -2 & 1 & 2 \end{array} \right| = -2\vec{i} -2\vec{j} -\vec{k}

\left| \vec{v_r} \times \vec{v_s} \right| = +\sqrt{(-2)^2+(-2)^2+(-1)^2}=+\sqrt{9}=3

d(r,s) = \frac{|9|}{3} = \frac{9}{3}=3

Están a una distancia de 3 unidades.