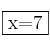Ecuaciones Logarítmicas

logaritmos
ecuaciones_logaritmicas

Resuelve la ecuación
$\log (x+3) - \log (x-6) = 1$

SOLUCIÓN

En primer lugar debemos repasar los pasos a seguir para resolver ecuaciones logarítmicas

$\log (x+3) - \log (x-6) = 1$

$\log (x+3) - \log (x-6) = \log (10)$

$\log \left( \frac{x+3}{x-6} \right) = \log (10)$

$\cancel{\log} \left( \frac{x+3}{x-6} \right) = \cancel{\log} (10)$

$\frac{x+3}{x-6} =10$

$x+3 =10 \cdot (x-6)$

$x = \frac{-63}{-9} \longrightarrow x=7$

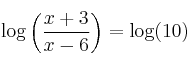
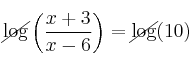
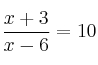
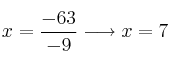
Verificamos que la solución no produce ningún logaritmo negativo (ni cero)
$\log (7+3) - \log (7-6) = 1$
Por tanto la solución es correcta: $\fbox{x=7}$

SOLUCIÓN

Palabras clave