Ejercicio Probabilidad 3350

| 2 |

Se lanzan 3 monedas, la primera de 50 céntimos, la segunda de 1 euro y la tercera de 2 euros. Se consideran los sucesos: Suceso A aparecen dos caras, suceso B aparece una cara en la moneda de 2 euros y el suceso C aparecen caras en las monedas de 50 céntimos y de un euro. Se pide de forma razonada:

– a) P(A/B)
– b) ¿Son independientes los sucesos B y C?

SOLUCIÓN

Las posibles opciones se muestran en el siguiente gráfico:

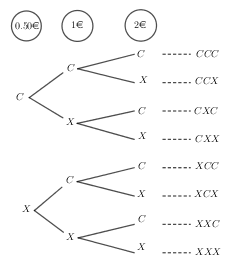
Tenemos los sucesos:

A = "sacar dos caras" \longrightarrow P(A) = \frac{3}{8}

B = "cara en la de 2€" \longrightarrow P(B) = \frac{4}{8}

C = "cara en laa de 0.50€ y 1€" \longrightarrow P(C) = \frac{2}{8}

– a) P(A/B) = \frac{P(A \cap B)}{P(B)}=\frac{2/8}{4/8}=0.5

– b) B y C independientes \Leftrightarrow P(B \cap C) = P(B)\cdot P(C)

P(B \cap C) = \frac{1}{8}
P(B) \cdot P(C) = \frac{4}{8} \cdot \frac{1}{8}= \frac{1}{8}

Por tanto, sí son independientes