Funciones gráfica
El beneficio esperado por una empresa, en los próximos 8 años, viene indicado por la función:
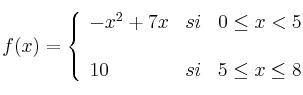
El tiempo (x) está expresado en años y el Beneficio f(x) viene expresado en millones de euros.
– a) Representa gráficamente la función
– b) Explica la evolución del beneficio en esos 8 años
– c) ¿Cuándo se espera un beneficio de 11,25 millones de euros?
SOLUCIÓN
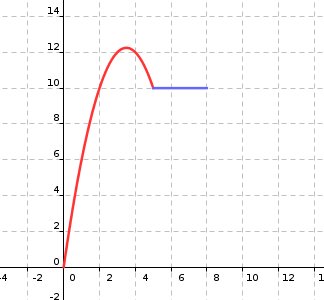
Representación gráfica
Se trata de una función a trozos: un trozo de 0 a 5 y otro de 5 a 8.
– Primer trozo: ![]() .
.
Es una parábola invertida (el coeficiente de la ![]() es negativo).
es negativo).
Obtengamos el vértice, cuya primera coordenada responde a la fórmula ![]() , siendo
, siendo ![]() el coeficiente de la
el coeficiente de la ![]() y
y ![]() el coeficiente de
el coeficiente de ![]()
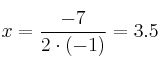
![]()
Por tanto: Vértice (3.5 , 12.25)
El Corte con los ejes nos suele ayudar a representar la parábola.
Si ![]() entonces
entonces ![]() . Corte
. Corte ![]()
Si ![]() entonces
entonces ![]() . Ecuación de 2º grado cuyas soluciones son 0 y 7.
. Ecuación de 2º grado cuyas soluciones son 0 y 7.
Por tanto los puntos de corte son ![]() y
y ![]() .
.
Debemos tener en cuenta, a la hora de representar gráficamente, que el ![]() está fuera de su dominio (de 0 a 5), por tanto no tenemos que representarlo.
está fuera de su dominio (de 0 a 5), por tanto no tenemos que representarlo.
Podemos asignar valores y obtener otros puntos que nos faciliten la representación gráfica. Debemos recordar que los valores 0 y 5 debemos asignarlos porque son los puntos de inicio y fin de trozo.
Podemos obtener las imágenes de 1,2 y 3. La simetría nos dará los puntos 4 y 5.

– Segundo trozo: ![]() . Es la función constante (recta horizontal por el 10) entre 5 y 8.
. Es la función constante (recta horizontal por el 10) entre 5 y 8.
Evolución del beneficio
El beneficio empieza en 0 cuando se crea la empresa y va aumentando hasta el año 3.5 en que alcanza el máximo: 12,25 millones de euros.
A partir del año 3,5 inicia un descenso (hasta los 10 millones) en el año 5.
Desde el año 5 hasta el 8 el beneficio se mantiene constante en 10 millones.
¿Cuándo se espera un beneficio de 11,25 millones de euros?
Analizando la gráfica se observa que hay dos momentos en que el beneficio es de 11,25 millones: uno antes del tercer año y otro después del cuarto año.
Para calcular exactamente en qué momento se alcanza ese beneficio, tan sólo tenemos que resolver la ecuación: ![]() . Por tanto:
. Por tanto:
![]()
Ecuación de segundo grado con dos soluciones: 2,5 y 4,5.
Por tanto el beneficio de 11,25 millones se alcanza en dos momentos:
– a los 2 años y medio
– a los 4 años y medio
Mensajes
11 de junio de 2008, 23:33, por dani
El beneficio esperado por una empresa, en los próximos 8 años, viene indicado por la función:
El tiempo (x) está expresado en años y el Beneficio f(x) viene expresado en millones de euros.
– a) Representa gráficamente la función
– b) Explica la evolución del beneficio en esos 8 años
– c) ¿Cuándo se espera un beneficio de 11,25 millones de euros?
Representación gráfica
Se trata de una función a trozos: un trozo de 0 a 5 y otro de 5 a 8.
– Primer trozo: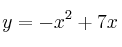 .
.
Es una parábola invertida (el coeficiente de la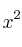 es negativo).
es negativo).
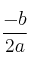 , siendo
, siendo 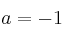 el coeficiente de la
el coeficiente de la 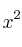 y
y 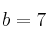 el coeficiente de
el coeficiente de 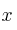
Obtengamos el vértice, cuya primera coordenada responde a la fórmula
Por tanto: Vértice (3.5 , 12.25)
El Corte con los ejes nos suele ayudar a representar la parábola.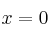 entonces
entonces 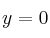 . Corte
. Corte 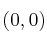
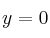 entonces
entonces 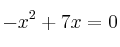 . Ecuación de 2º grado cuyas soluciones son 0 y 7.
. Ecuación de 2º grado cuyas soluciones son 0 y 7.
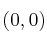 y
y 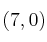 .
.
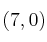 está fuera de su dominio (de 0 a 5), por tanto no tenemos que representarlo.
está fuera de su dominio (de 0 a 5), por tanto no tenemos que representarlo.
Si
Si
Por tanto los puntos de corte son
Debemos tener en cuenta, a la hora de representar gráficamente, que el
Podemos asignar valores y obtener otros puntos que nos faciliten la representación gráfica. Debemos recordar que los valores 0 y 5 debemos asignarlos porque son los puntos de inicio y fin de trozo.
Podemos obtener las imágenes de 1,2 y 3. La simetría nos dará los puntos 4 y 5.
– Segundo trozo: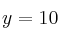 . Es la función constante (recta horizontal por el 10) entre 5 y 8.
. Es la función constante (recta horizontal por el 10) entre 5 y 8.
Evolución del beneficio
El beneficio empieza en 0 cuando se crea la empresa y va aumentando hasta el año 3.5 en que alcanza el máximo: 12,25 millones de euros.
A partir del año 3,5 inicia un descenso (hasta los 10 millones) en el año 5.
Desde el año 5 hasta el 8 el beneficio se mantiene constante en 10 millones.
¿Cuándo se espera un beneficio de 11,25 millones de euros?
Analizando la gráfica se observa que hay dos momentos en que el beneficio es de 11,25 millones: uno antes del tercer año y otro después del cuarto año.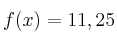 . Por tanto:
. Por tanto:
Para calcular exactamente en qué momento se alcanza ese beneficio, tan sólo tenemos que resolver la ecuacion:
Ecuación de segundo grado con dos soluciones: 2,5 y 4,5.
Por tanto el beneficio de 11,25 millones se alcanza en dos momentos:
– a los 2 años y medio
– a los 4 años y medio